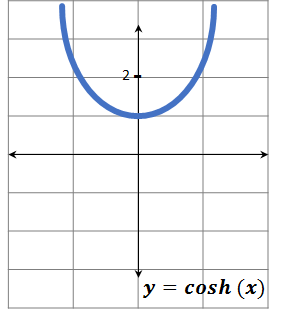Funciones hiperbólicas

Las funciones hiperbólicas se definen a través de expresiones algebraicas que incluyen funciones exponenciales e^x y su función inversa e^-x , donde e es la constante de Euler (o como se le conoce comúnmente “número e”), cuyo valor aproximado es 2,718281. Las funciones hiperbólicas básicas son seno hiperbólico (sinh) y el coseno hiperbólico (cosh), de éstos se derivan la función de tangente hiperbólica (tanh). Las otras funciones: cotangente (coth), secante (sech) y cosecante (csch), son las inversas de las tres anteriores respectivamente.

Definición

Se denominan funciones hiperbólicas al coseno hiperbólico (cosh), seno hiperbólico (senh) y las funciones que se obtienen a partir de ellas, como son la tangente hiperbólica (tanh) y sus respectivas inversas:

Coseno hiperbólico

Cosh (x) = (e^x + e^-x) / 2

Es una función par.

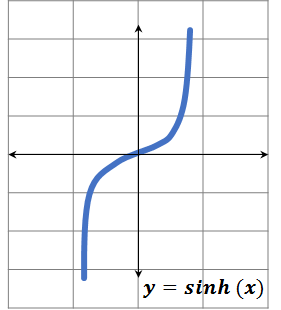
Seno hiperbólico

senh (x) = (e^x – e^-x) / 2

Es una función impar.

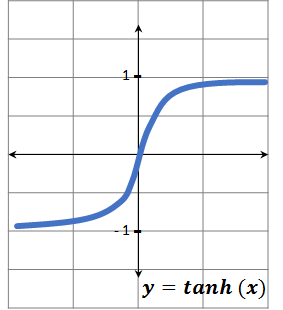
Tangente hiperbólica

Tanh (x) = senh (x) / cosh (x) = (e^x – e^-x) / (e^x + e^-x) = (e^2x – 1) / (e^2x + 1)

Es una función impar.

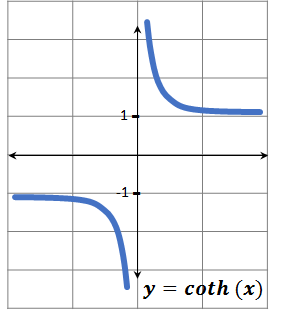
Cotangente hiperbólica

Coth (x) = cosh (x) / senh (x) = (e^x + e^-x) / (e^x – e^-x) = (e^2x + 1) / (e^2x – 1)

Definida sobre R* y más generalmente sobre C*; es una función impar.

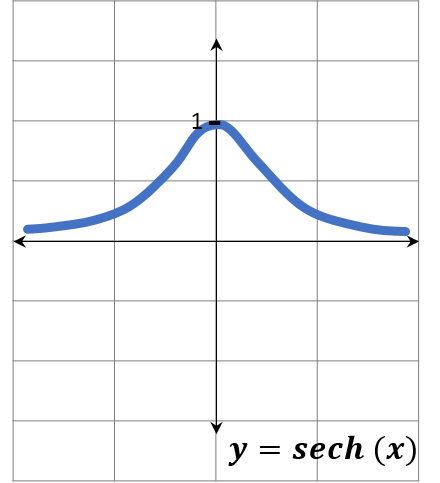
Secante hiperbólica

Sech (x) = 1 / cosh (x) = 2 / (e^x + e^-x) =  2e^x / (e^2x + 1)

Es una función par.

Cosecante hiperbólica

Csch (x) = 1 / senh (x) = 2 / (e^x – e^-x) =  2e^x / (e^2x – 1)

Definida sobre R* y más generalmente sobre C*; es una función impar.

Demostración geométrica

Las funciones sinh y cosh satisfacen la ecuación de la hipérbola x² – y² = 1.

Suponiendo que x = cosh (t) e y = sinh (t) y considerando que:

Cosh (t) = (e^t + e^-t) / 2 y senh (t) = (e^t – e^-t) / 2

Sustituimos en la ecuación de la hipérbola

[(e^t + e^-t) / 2]² – [(e^t – e^-t) / 2]² = 1

[(e^2t +2e^te^-t + e^-2t) / 4] – [(e^2t – 2e^te^-t + e^-2t) / 4] = 1

Como e^te^-t = e^{t – t} = e⁰ = 1, tenemos:

[(e^2t + 2 + e^-2t) / 4] – [(e^2t – 2 + e^-2t) / 4] = 1

Restamos ya que tienen el mismo denominador:

[(e^2t + 2 + e^-2t)  – (e^2t – 2 + e^-2t)] / 4 = 1

(e^2t + 2 + e^-2t  – e^2t + 2 – e^-2t) / 4 = 1

(e^2t – 2 + e^-2t  – e^2t – 2 – e^-2t) / 4 = 1

4 / 4 = 1

1 = 1

Que es lo que queríamos demostrar.