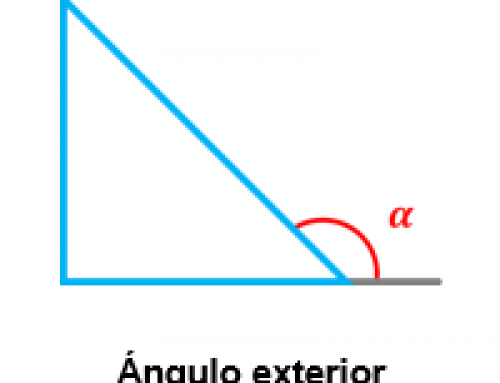
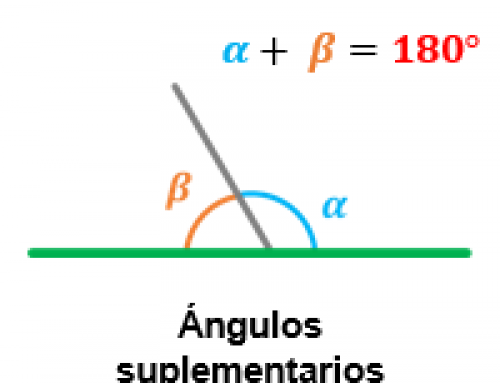
Ángulos verticales
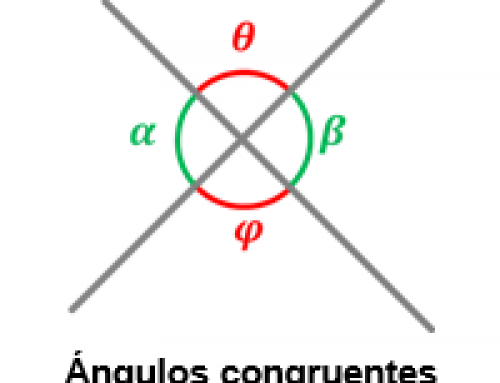
En general, los ángulos verticales son aquellos ángulos opuestos uno al otro cuando dos líneas se cruzan. Estos son siempre congruentes.
Definición
Los ángulos verticales son un par de ángulos (no adyacentes) opuestos uno al otro cuando dos líneas se cruzan.
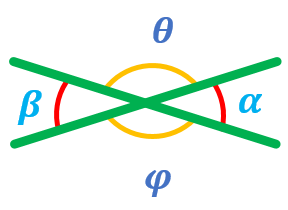
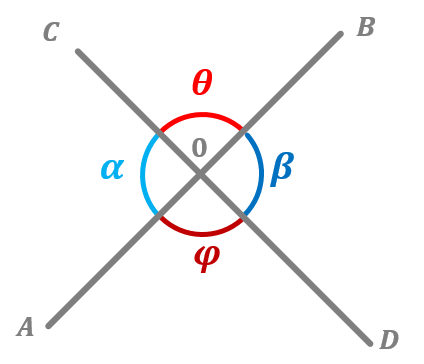
Figura I.
Cuando dos líneas de interceptan se forman 4 ángulos. Aquellos que son opuestos uno al otro son ángulos verticales, estos son siempre congruentes (iguales). Por lo tanto, en la Figura I:
Teorema de los ángulos verticales
Los ángulos verticales son siempre congruentes.
Demostración
Sean dos rectas AB y CD que se interceptan en el punto 0. Demostraremos que:
De la figura observamos que θ y β son suplementarios, esto es:
β y φ también son suplementarios, así:
Igualando (1) y (2) tenemos:
Por lo tanto:
Análogamente:
Como:
Entonces:
Por lo tanto:
Ejercicios
1. Hallar los ángulos α y β si estos son complementarios y el menor es 40⁰ más pequeño que el otro.
Como α y β son complementarios, sus medidas suman 90⁰, es decir:
Sea α el más pequeño, por lo tanto:
De (1) despejamos β y luego sustituimos el resultado en (2):
Ahora despejamos α:
Con este resultado calculamos β usando la ecuación (3):
2. Hallar α y β si estos son suplementarios y el mayor es 20⁰ más grande que tres veces el otro.
Como α y β son suplementarios, sus medidas suman 180⁰, es decir:
Sea α el más grande, por lo tanto:
Es decir, α es 20⁰ más grande que 3 veces β.
De (1) despejamos β y luego sustituimos el resultado en (2):
Ahora despejamos α:
Con este resultado calculamos β usando la ecuación (3):