Vector suma

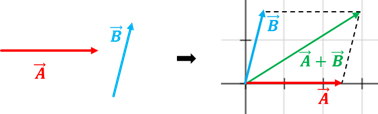
La idea de vector suma aparece cuando realizamos una operación de suma de vectores. Por ejemplo, si utilizamos el método del triángulo para sumar dos vectores A y B, debemos dibujarlos de manera consecutiva (respetando sus módulos, direcciones y sentidos), haciendo que el origen de B  coincida con el extremo A; el vector suma A + B tendrá como origen, el origen A y como extremo el origen de B.

Definición

Sean dos vectores A y B, el vector suma se obtiene al sumar el vector A con el vector B, es decir, al sumar las componentes de cada vector:

A + B = (A_x + B_x, A_y + B_y, A_z + B_z)

Ejemplo: Sean A = (3, 2, -4) y B = (-3, 2, 7), calcula el vector A + B.

A + B = ( 3 + (-3), 2 + 2, -4 – 7) = (0, 4, 3)

Suma de dos vectores con la misma dirección y el mismo sentido

Sean A y B:

Para obtener el vector suma seguimos los siguientes pasos:

1. Dibujamos el vector B a continuación del vector A, de manera que sean consecutivos, respetando sus módulos, direcciones y sentidos.
2. El vector suma A + B tiene como módulo la suma de los módulos de ambos, la misma dirección y el mismo sentido de los vectores dados.

Suma de dos vectores con la misma dirección y el sentido opuesto

Sean A y B:

Para obtener el vector suma seguimos los siguientes pasos:

1. Dibujamos el vector B a continuación del vector A, de manera que sea consecutivos, respetando sus módulos, direcciones y sentidos.
2. .El vector suma A + B tiene como módulo la diferencia de los módulos de ambos, la misma dirección y el sentido del vector mayor.

Suma de dos vectores con distinta dirección

Para sumar dos vectores A  y B que forman un ángulo entre sí, se usan dos métodos: el método del triángulo y el método del paralelogramo.

Método del triangulo

1. Dibujamos los vectores de forma consecutiva, es decir, el origen de B tiene que coincidir con el extremo A.
2. El vector suma A + B tiene como origen, el origen de A  y como extremo, el de B.

Ley o método de paralelogramo

1. Dibujamos el vector A en el origen de un plano cartesiano respetando su módulo, dirección y sentido.
2. Dibujamos en el origen de A, el vector B respetando su módulo, dirección y sentido.
3. Se trazan rectas paralelas a cada vector formando un paralelogramo.
4. El vector resultante será la diagonal del paralelogramo que inicia en el origen del plano cartesiano.

Propiedades del vector suma

Propiedad conmutativa

Sean dos vectores A y B; de acuerdo a la ley del paralelogramo, la diagonal AC representa el vector suma S:

De acuerdo a la figura:

S = A + B = B + A

La suma de vectores es conmutativa.

Propiedad asociativa

Sean tres vectores A, B y C y el vector suma S = A + B + C   

De acuerdo a la figura:

AB = AD + DB   →  S = A + (B + C)  

Y

AB = AC + CB   →  S = (A + B) + C  

Por lo tanto

A + (B + C) = (A + B) + C     

La suma de vectores es asociativa.

Propiedad distributiva

La suma de vectores es distributiva respecto a la multiplicación por escales:

(A + B)μ = μA + μB